Concept of Pointwise Mutual Information in NLP

In previous lessons, we have learned about reducing words to their base form. However, there may be a situation where a single term comprising multiple words will be reduced to its base forms but as it is a single term so reducing it into multiple words would be inaccurate.

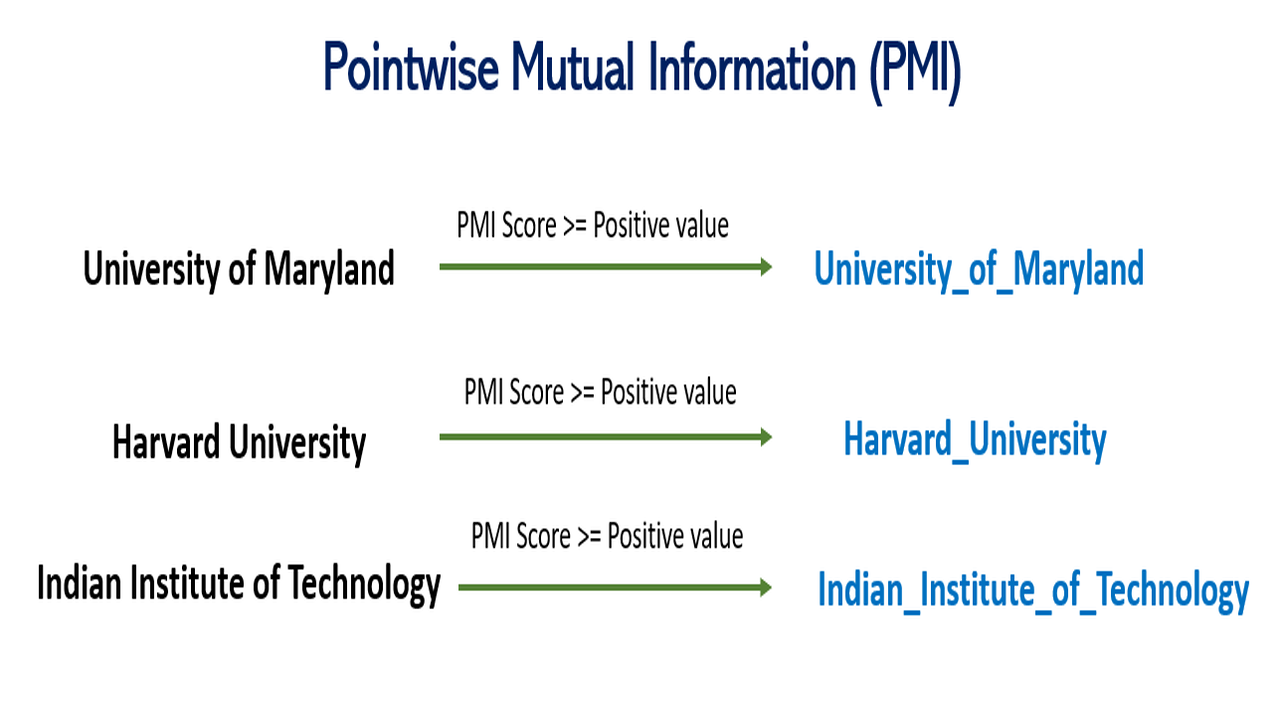
For example, in a document, there are names of certain universities such as Harvard University, University of Maryland, Indian Institute of Technology, etc. Now, when we tokenize this document, all these university names will be reduced to their base words/forms such as ‘Harvard‘, ‘University’, ‘University’, ‘of’, ‘Maryland’, ‘Indian’, ‘Institute’, ‘of’, ‘Technology’ and so on. But we don’t want this as the entire university name should be represented by one token logically.

In order to solve this critical issue, we could either replace these university names with a single term such as ‘University of Maryland’ could be replaced by ‘UOM’. But this seems to be a purely manual process. To replace university names in this way, we would need to read the entire corpus to look up such terms.

However, in Natural Language Processing domain, there is a popular metric named pointwise mutual information, also called the PMI. It is a statistical measure to calculate the association between two words in a given corpus. PMI is calculated by comparing the probability of the co-occurrence of two words with their individual probabilities of occurrence.

The formula for PMI is as follows:

PMI(x,y) = log(P(x,y) / (P(x) * P(y)))

where

• x and y are two words being considered,
• P(x) is the probability of the occurrence of word x in the corpus,
• P(y) is the probability of the occurrence of word y in the corpus, and
• P(x,y) is the probability of the co-occurrence of words x and y in the corpus.

For terms with three words, the formula becomes:

PMI(z, y, x) = log [(P(z,y,x))/(P(z)P(y)P(x))]

                                    = log [(P(z|y, x)*P(y|x))*P(x)/(P(z)P(y)P(x))]

                         = log [(P(z|y, x)*P(y|x))/([P(z)P(y))]

PMI values can range from -infinity to infinity. Positive PMI values indicate that the words have a strong association, while negative values indicate that the words are unlikely to appear together.

For example, consider a small corpus of text:

“The cat sat on the mat. The dog sat on the mat.“

Let’s calculate the PMI of the words “cat” and “mat“:

P(cat) = 1/6 P(mat) = 2/6 = 1/3 P(cat,mat) = 1/6

PMI(cat,mat) = log((1/6) / ((1/6)*(1/3))) = log(3) = 1.0986

The positive PMI value suggests that “cat” and “mat” have a strong association and are likely to appear together.

In real-time problems, calculating PMI for longer terms (length>2) is still very costly for any relatively large corpus of text. We can either go for calculating it only for a two-word term or choose to skip it if we know that there are only a few occurrences of such terms.

PMI is commonly used in various NLP tasks such as information retrieval, topic modeling, and sentiment analysis, to identify and analyze the relationships between words in a corpus.